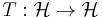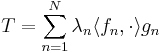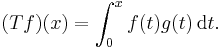Compact operator
In functional analysis, a branch of mathematics, a compact operator is a linear operator L from a Banach space X to another Banach space Y, such that the image under L of any bounded subset of X is a relatively compact subset of Y. Such an operator is necessarily a bounded operator, and so continuous.
Any bounded operator L that has finite rank is a compact operator; indeed, the class of compact operators is a natural generalisation of the class of finite-rank operators in an infinite-dimensional setting. When Y is a Hilbert space, it is true that any compact operator is a limit of finite-rank operators, so that the class of compact operators can be defined alternatively as the closure in the operator norm of the finite-rank operators. Whether this was true in general for Banach spaces (the approximation property) was an unsolved question for many years; in the end Per Enflo gave a counter-example.
The origin of the theory of compact operators is in the theory of integral equations, where integral operators supply concrete examples of such operators. A typical Fredholm integral equation gives rise to a compact operator K on function spaces; the compactness property is shown by equicontinuity. The method of approximation by finite-rank operators is basic in the numerical solution of such equations. The abstract idea of Fredholm operator is derived from this connection.
Contents |
Equivalent formulations
A bounded operator T is compact if and only if any of the following is true
- Image of the unit ball in X under T is relatively compact in Y.
- Image of any bounded set under T is relatively compact in Y.
- Image of any bounded set under T is totally bounded in Y.
- there exists a neighbourhood of 0,
 , and compact set
, and compact set 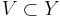 such that
such that 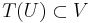 .
. - For any sequence
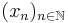 from the unit ball in X, the sequence
from the unit ball in X, the sequence 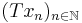 contains a Cauchy subsequence.
contains a Cauchy subsequence.
Note that if a linear operator is compact, then it is easy to see that it is bounded, and hence continuous.
Important properties
In the following, X, Y, Z, W are Banach spaces, B(X, Y) is the space of bounded operators from X to Y with the operator norm, K(X, Y) is the space of compact operators from X to Y, B(X) = B(X, X), K(X) = K(X, X), 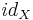 is the identity operator on X.
is the identity operator on X.
- K(X, Y) is a closed subspace of B(X, Y): Let Tn, n ∈ N, be a sequence of compact operators from one Banach space to the other, and suppose that Tn converges to T with respect to the operator norm. Then T is also compact.
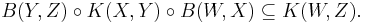 In particular, K(X) forms a two-sided operator ideal in B(X).
In particular, K(X) forms a two-sided operator ideal in B(X).
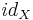 is compact if and only if X has finite dimension.
is compact if and only if X has finite dimension.
- For any T ∈ K(X),
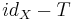 is a Fredholm operator of index 0. In particular,
is a Fredholm operator of index 0. In particular, 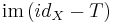 is closed. This is essential in developing the spectral properties of compact operators. One can notice the similarity between this property and the fact that, if M and N are subspaces of a Banach space where M is closed and N is finite dimensional, then M + N is also closed.
is closed. This is essential in developing the spectral properties of compact operators. One can notice the similarity between this property and the fact that, if M and N are subspaces of a Banach space where M is closed and N is finite dimensional, then M + N is also closed.
- Any compact operator is strictly singular, but not vice-versa.[1]
Origins in integral equation theory
A crucial property of compact operators is the Fredholm alternative, which asserts that the existence of solution of linear equations of the form
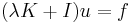
behaves much like as in finite dimensions. The spectral theory of compact operators then follows, and it is due to Frigyes Riesz (1918). It shows that a compact operator K on an infinite-dimensional Banach space has spectrum that is either a finite subset of C which includes 0, or the spectrum is a countably infinite subset of C which has 0 as its only limit point. Moreover, in either case the non-zero elements of the spectrum are eigenvalues of K with finite multiplicities (so that K − λI has a finite dimensional kernel for all complex λ ≠ 0).
An important example of a compact operator is compact embedding of Sobolev spaces, which, along with the Gårding inequality and the Lax–Milgram theorem, can be used to convert an elliptic boundary value problem into a Fredholm integral equation.[2] Existence of the solution and spectral properties then follow from the theory of compact operators; in particular, an elliptic boundary value problem on a bounded domain has infinitely many isolated eigenvalues. One consequence is that a solid body can vibrate only at isolated frequencies, given by the eigenvalues, and arbitrarily high vibration frequencies always exist.
The compact operators from a Banach space to itself form a two-sided ideal in the algebra of all bounded operators on the space. Indeed, the compact operators on a Hilbert space form a maximal ideal, so the quotient algebra, known as the Calkin algebra, is simple.
Compact operator on Hilbert spaces
An equivalent definition of compact operators on a Hilbert space may be given as follows.
An operator  on a Hilbert space
on a Hilbert space 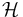
is said to be compact if it can be written in the form
where 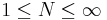 and
and  and
and  are (not necessarily complete) orthonormal sets. Here,
are (not necessarily complete) orthonormal sets. Here,  is a sequence of positive numbers, called the singular values of the operator. The singular values can accumulate only at zero. The bracket
is a sequence of positive numbers, called the singular values of the operator. The singular values can accumulate only at zero. The bracket 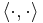 is the scalar product on the Hilbert space; the sum on the right hand side converges in the operator norm.
is the scalar product on the Hilbert space; the sum on the right hand side converges in the operator norm.
An important subclass of compact operators are the trace-class or nuclear operators.
Completely continuous operators
Let X and Y be Banach spaces. A bounded linear operator T : X → Y is called completely continuous if, for every weakly convergent sequence 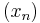 from X, the sequence
from X, the sequence 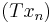 is norm-convergent in Y (Conway 1985, §VI.3). Compact operators on a Banach space are always completely continuous. If X is a reflexive Banach space, then every completely continuous operator T : X → Y is compact.
is norm-convergent in Y (Conway 1985, §VI.3). Compact operators on a Banach space are always completely continuous. If X is a reflexive Banach space, then every completely continuous operator T : X → Y is compact.
Examples
- For some fixed g ∈ C([0, 1]; R), define the linear operator T by
- That the operator T is indeed compact follows from the Ascoli theorem.
- More generally, if Ω is any domain in Rn and the integral kernel k : Ω × Ω → R is a Hilbert—Schmidt kernel, then the operator T on L2(Ω; R) defined by
- is a compact operator.
- By Riesz's lemma, the identity operator is a compact operator if and only if the space is finite dimensional.
See also
- Spectral theory of compact operators
- Fredholm operator
- Fredholm integral equations
- Fredholm alternative
- Compact embedding
- Strictly singular operator
Notes
- ^ N.L. Carothers, A Short Course on Banach Space Theory, (2005) London Mathemaitcal Society Student Texts 64, Cambridge University Press.
- ^ William McLean, Strongly Elliptic Systems and Boundary Integral Equations, Cambridge University Press, 2000
References
- Conway, John B. (1985). A course in functional analysis. Springer-Verlag. ISBN 3-540-96042-2
- Renardy, Michael and Rogers, Robert C. (2004). An introduction to partial differential equations. Texts in Applied Mathematics 13 (Second ed.). New York: Springer-Verlag. p. 356. ISBN 0-387-00444-0. (Section 7.5)
- Kutateladze, S.S. (1996). Fundamentals of Functional Analysis. Texts in Mathematical Sciences 12 (Second ed.). New York: Springer-Verlag. p. 292. ISBN 978-0-7923-3898-7.